2024/8/26:
1.FPGA FIR滤波器方法
FIR为有限长滤波器,可以简单利用卷积方式进行实现,实现方法有1.直接式2.并行3.分布式算法4.IP
原理图:
1 直接式
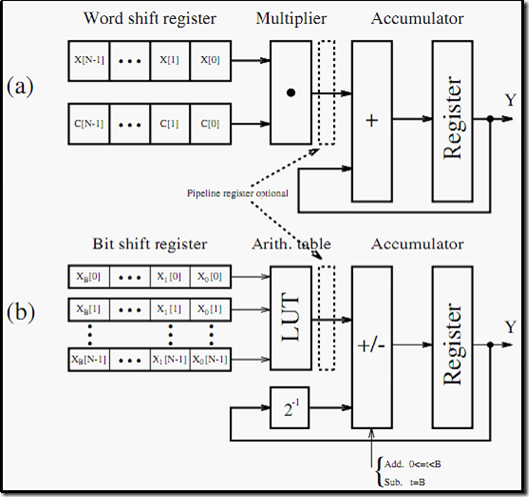
2.并行
3.分布式
4.IP调用
结果图
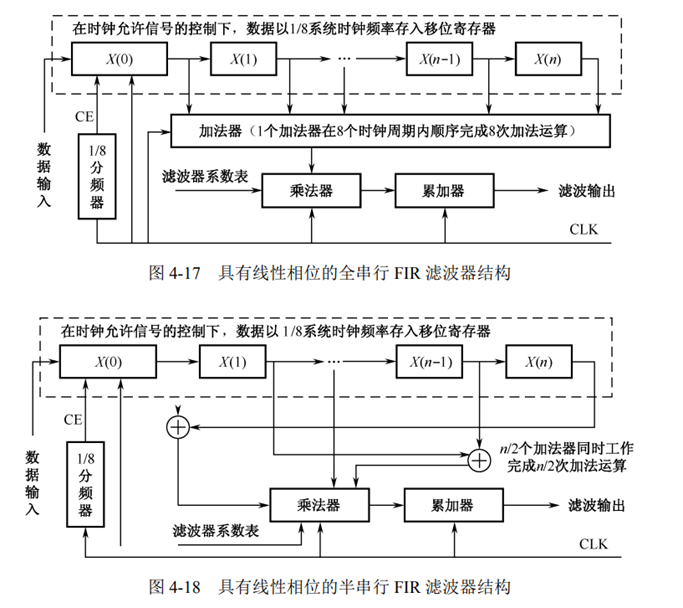
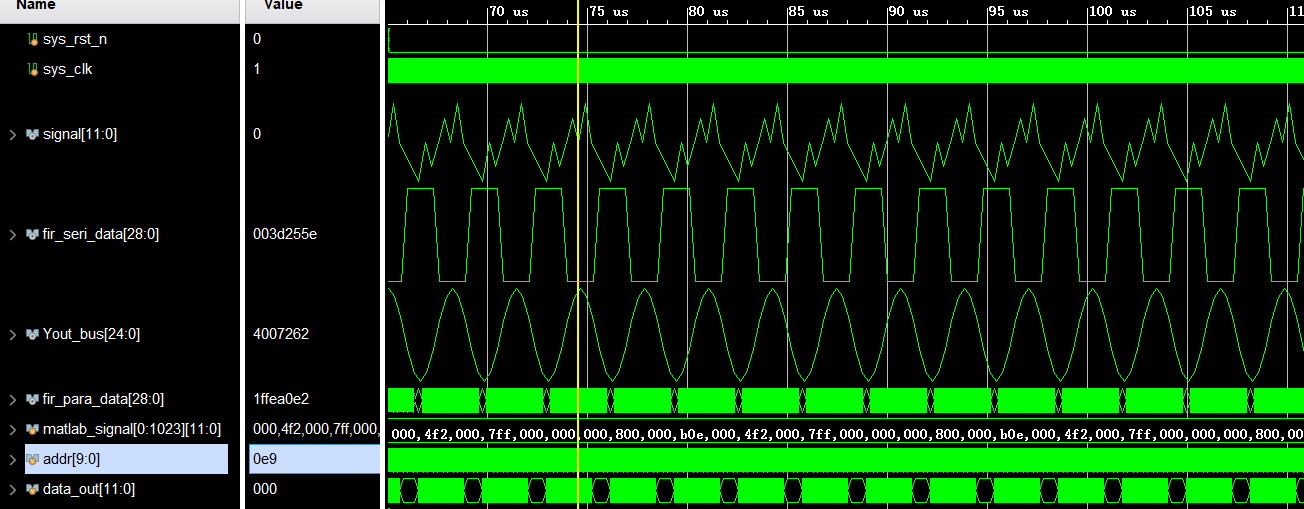
1.串行FIR滤波器也是直接式FIR滤波器是通过多个数相加再相乘,与串行相比调用资源少,但是用延时换取电路资源,因此16阶滤波器需要八个延时,数据必须比时钟信号慢八倍才可以,该程序结果需要去掉高三位符号位才能得到最好的结果
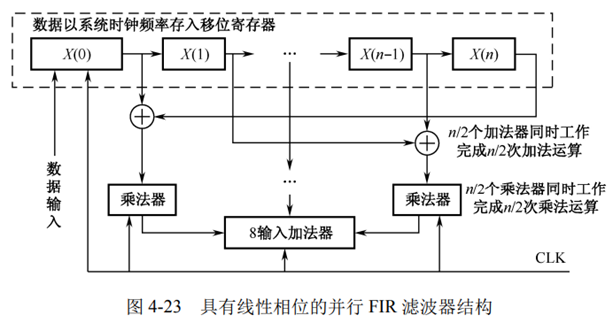
2.并行FIR滤波器有八个乘法器,因此可以与信号时钟频率相等的情况下进行
3.分布式暂未实现
[分布式算法原理 - alifpga - 博客园 (cnblogs.com)](https://www.cnblogs.com/alifpga/p/9227953.html)
4.IP实现结果不对
2.MATLAB实现方法
1.fir1
需要清楚的是,使用 fir1 函数设计滤波器时,实际上是采用了 窗函数设计方法。
fir1 函数的语法形式有以下几种:
b=fir1(n,wn)
b=fir1(n,wn,’ftype’)
b=fir1(n,wn,’ftype’,window)
b=fir1(…,’noscale’)
其中,各项参数的意义及作用如下所述。
(1)b:返回的 FIR 滤波器单位脉冲响应,脉冲响应为偶对称,长度为 n+1。
(2)n:滤波器的阶数,需要注意的是,设计出的滤波器长度为 n+1。
(3)wn:滤波器截止频率,需要注意的是,wn 的取值范围为 0<
2.kaiserord
在实际工程设计中,可 根据相关算法,先选择过渡带、纹波参数,并可根据这些参数计算出凯塞窗的 b 值,以及滤 波器阶数。
kaiserord 函数的语法形式为:
[n,wn,beta,filtype] =kaiserord(f,a,dev,fs)
其中,各项参数的意义及作用如下所述。
(1)f 及 fs:如果 f 是一个向量,则其中的元素为待设计滤波器的过渡带的起始点和结束 点;如果没有 fs 参数,则 f 中元素的取值范围为 0~1,即相对于抽样频率一半的归一化频率; 如果有 fs 参数,则 fs 为信号抽样频率,f 中元素即实际的截止频率。例如,需要设计滤波器 的过滤带宽为 1000~1200 Hz、2000~2100 Hz;信号抽样频率为 8000 Hz;若没有设置 fs 参 数,则 f= [0.25 0.3 0.5 0.525];若设置 fs 为 8000,则 f= [1000 12000 2000 2100]。
(2)a:a 是一个向量,参数 f 确定了待设计滤波器的过渡带,向量 a 用于指定这些频率 段的理想幅度值。如果要求某个频带为通带,则设置为 1,阻带则设置为 0。a 与 f 的对应关 系为:a 的第一个参数 a1 对应为 f 中的 0~f1 频段,第二个参数 a2 对应 f 中的 f2~f3 频段, 后续对应关系以此类推。例如,对于上面讲述 f 及 fs 参数的例子,设置 a=[1 0 1],则表示需 要设计带阻滤波器。可以看出,由 f 及 a 可以表示滤波器的类型。
(3)dev:dev 是一个向量,用于指定通带或阻带内的容许误差。同样是上述例子,要求 通带容许误差为 0.01,阻带容许误差为 0.02,则 dev=[0.01 0.02 0.01]。
(4)n:返回值 n 为 kaiserord 函数根据滤波器要求得到的满足设计的最小阶数。
(5)wn:返回值 wn 是一个向量,为 kaiserord 函数计算得到的滤波器截止频率点。
(6)beta:返回值 beta 是根据滤波器要求,为 kaiserord 函数计算得到的 b 值。
(7)ftype:返回值 ftype 是根据设计要求获得的滤波器类型参数。 关于该函数的应用示例,在讲述完最优滤波器设计函数 firpm 后一并给出
3.fir2
fir2 最大误差最小准则下的最优滤波器设计方法
任意响应滤波器的设计。所谓任意响应滤波器,是指滤波 器的幅频响应在指定的频段范围内有不同的幅值,如在 0~0.1 的幅值为 1,在 0.2~0.4 频段 内的幅值为 0.5,在 0.6~0.7 频段内的幅值为 1 等。MATLAB 提供的 fir2 函数能够完成这种 滤波器的设计。fir2 函数的算法是:首先根据要求的幅频响应的向量形式进行插值,而后进行 傅里叶变换得到理想滤波器的单位脉冲响应,最后利用窗函数对理想滤波器的单位脉冲响应 进行截短处理,由此获得 FIR 滤波器的系数。fir2 函数的 6 种语法形式如下:
b=fir2(n,f,m)
b=fir2(n,f,m,window)
b=fir2(n,f,m,npt)
b=fir2(n,f,m,npt,window)
b=fir2(n,f,m,npt,lap)
b=fir2(n,f,m,npt,lap,window)
其中各项参数的意义及作用如下所述。
(1)n 及 b:n 为滤波器的阶数,与 fir1 函数类似;返回值 b 为滤波器系数,其长度为 n+1。 同时,根据 FIR 滤波器的结构特点,当设计的滤波器在归一化频率为 1 处的幅度值不为 0 时, n 不能为奇数。
(2)f 及 m:f 是一个向量,其取值为 0~1,对应于滤波器的归一化频率。m 是长度与 f 相同的向量,用于设置对应频段范围内的幅值。例如,要求设计的滤波器在 0~0.125 的幅值 为 1,在 0.125~0.25 的幅值为 0.5,在 0.25~0.5 的幅值为 0.25,在 0. 5~1 的幅值为 0.125, 则 f 可以表示为[0 0.125 0.125 0.25 0.25 0.5 0.5 1],m 可以表示为[1 1 0.5 0.5 0.25 0.25 0.125 0.125 ]。
(3)window:window 是一个向量,用于指定窗函数的种类,其长度为滤波器的长度,即 n+1,当没有指定窗函数时,默认为海明窗函数。
(4)npt:npt 是一个正整数,用于指定在对幅频响应进行插值时的插值点个数,其默认 值为 512。
(5)lap:lap 是一个正整数,用于指定对幅频响应进行插值时,将不连续点转变成连续点 时的点数,其默认值为 25。
4.Firpm
b = firpm(n,f,a)
b = firpm(n,f,a,w)
b = firpm(n,f,a,'ftype')
b = firpm(n,f,a,w,'ftype')
[b,delta] = firpm(...)
firpm 函数中各项参数的意义及作用如下:
(1)n 及 b:n 为滤波器的阶数,与 fir1 函数类似,返回值 b 为滤波器系数,其长度为 n+1。
(2)f 及 a:f 是一个向量,取值为 0~1,对应于滤波器的归一化频率。a 是长度与 f 相同 的向量,用于设置对应频段范围内的幅值。对于 f 及 a 之间的关系用图形表示更为清楚,设 置 f=[0 0.3 0.4 0.6 0.7 1],a=[0 1 0 0 0.5 0.5],则 f 及 a 所表示的理想幅频响应如图 4-13 所示, 由图 4-13 可知,firpm 实际上也可以设计任意幅频响应的滤波器。
(3)w:w 是长度为 f 长度的 1/2 的向量,表示在设计滤波器时实现对应频段幅值的权值。 用下标表示向量的元素,则 w0 对应的是 f0~f1 频段,w1 对应的是 f2~f3 频段,以此类推。 权值越高,在实现时相应频段的幅值越接近理想状态。
(4)ftype:ftype 用于指定滤波器的结构类型, 若没有设置该参数,则表示设计偶对称脉冲响应 的滤波器;若设置为“hilbert”,则表示设计奇对 称结构的滤波器,即具有 90°相移特性;若设置 为“differentiator”,则表示设计奇对称结构的滤 波器,且设计时针对非零幅度的频带进行了加权 处理,使滤波器的频带越低,幅值误差越小。
(5)delta:delta 为返回的滤波器的最大纹 波值。 经过上面的介绍,我们发现 firpm 函数好像 是万能的,既能设计出最优滤波器,又能设计任意幅频响应的滤波器,还能设计出 90°相移 的滤波器
5.FDATOOL
通过仿真可以明显看出除了滤波器系数的量化效应,运算中的 字长效应也会对滤波效果产生明显的影响。在本例中,为什么在 FPGA 实现过程中没产生运 算字长效应呢?首先,FIR 滤波器不是一个闭环系统,不会像 IIR 滤波器那样随着运算的进行, 不断增加运算字长;其次,在本例中的每一步运算,均通过增加字长保证了运算的准确性, 即没有进行任何截位处理。





文章评论