2024/8/26：
1.滤波器方法

IIR滤波器主要在于具有反馈，反馈如何进行是需要注意的，由于反馈如何进行，主要方法为两种，一种是分为零点与极点分别进行，另一种为将反馈分解进行，少有的方法是合理运用模拟向数字滤波器变换的方法，如双线性变换等。

IIR 滤波器有直接 I 型、直接Ⅱ型、级联型及并联型 4 种常用的结构

1.1.直接式

零点系数的 PFGA 实现可完全看成一个 FIR 滤波器，因此可完全采用实现 FIR 滤波器时所介绍的方法。需要注意的是，由于 IIR 滤波器的反馈结构特性，实现零点系数及极点系数的运算需要满足严格的时序要求。也就是说，要求在计算零/极点时不出现延时，这一结构特点实际上限制了系统的运行速度。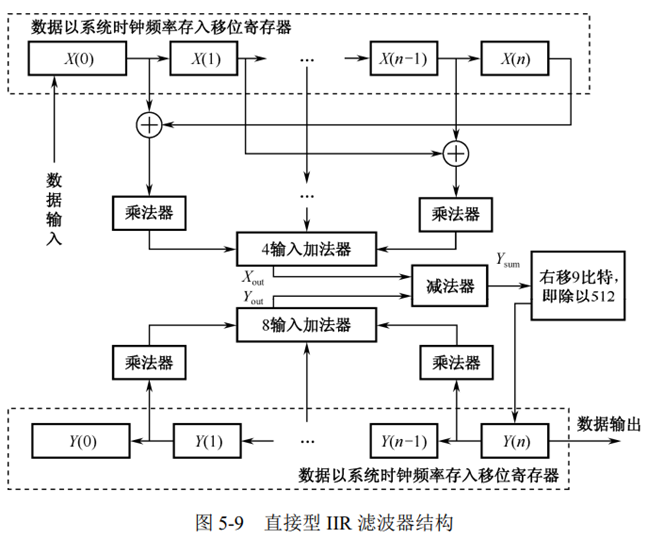

1.2.级联式

注重分解即可，将大的反馈结构分解为小的反馈结构

结果图

2.1.直接式

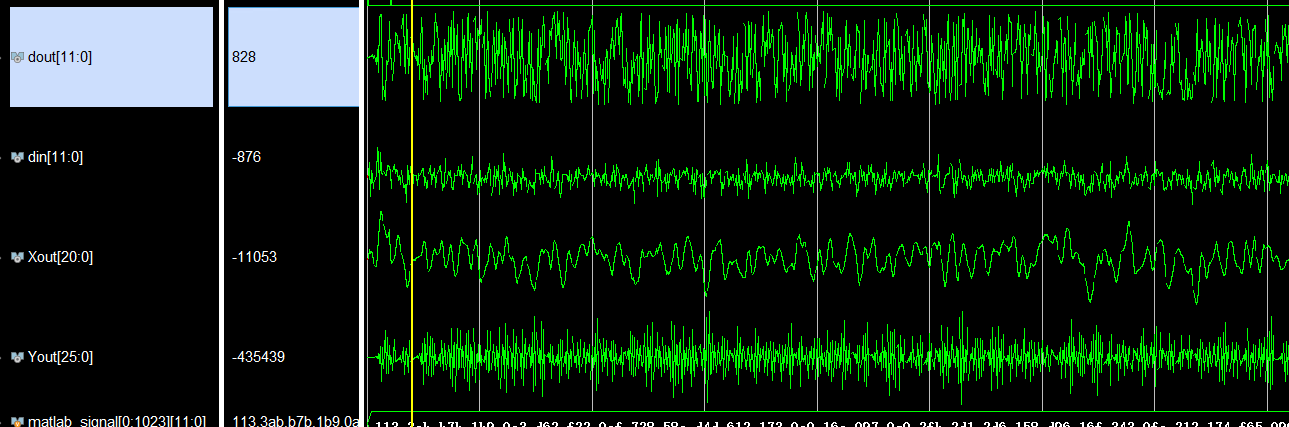
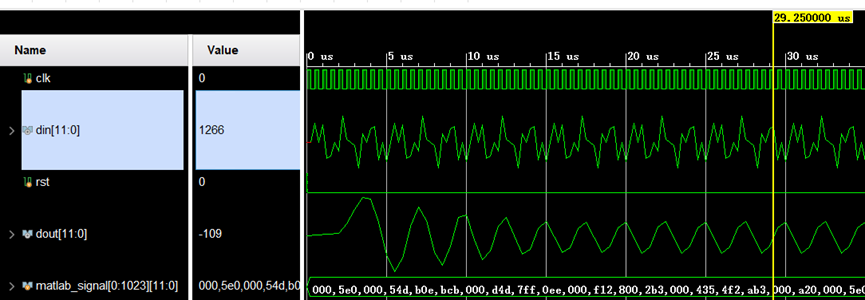
只实现了零点的，极点并未实现，初步猜测是因为仿真时的时序问题，调试了很久没有成功遂放下一段时间以后再看
din为读取TXT程序，dout为输出，XOUT为零点结果，YOUT为极点结果

2.2.级联型

## 2.软件方法以及特性

### 1.巴特沃斯

巴特沃斯低通滤波器的特点是通带的频率响应曲线较为平滑

MATLAB 提供了直接根据滤波器阶数计算巴特沃斯低通滤波器的零点、极点及增益的函数，即

[z,p,k]=buttap(N)

其中，N 表示巴特沃斯低通滤波器阶数，函数返回值 z、p、k 分别表示零点、极点和增益。

### 2.切比雪夫

如果将指标的精度要求均匀地分布在整个通带内，或者均匀地分布在阻带内，或者同时均匀分布在通带和阻带内，则可以设计出满足设计要求、阶数又比较低的滤波器。这就要求逼近函数具有等纹波特征。切比雪夫 I 型低通滤波器在通带内幅度特性是等纹波的，在阻带内是单调的；切比雪夫Ⅱ型低通滤波器则正好相反，它在通带内是单调的，在阻带内是等纹波的

MATLAB 提供了直接根据滤波器阶数计算切比雪夫 I 型低通滤波器的零点、极点及增益的函数，即

[z,p,k]=chelap(N,rP)

其中，N 表示滤波器阶数，rp 为通带纹波，函数返回值 z、p、k 分别表示零点、极点和增益。